.
3.6 Určité integrály
Teorii naleznete v kapitole 6.5 Multimediální encyklopedie nebo v kapitole 3.6 Breviáře
Příklad 1
Vypočítejte určitý integrál .
Řešení
Obvyklý postup při výpočtu určitého integrálu 
zahrnuje dva kroky:
a) výpočet odpovídajícího integrálu neurčitého (primitivní funkce) F(x) = ∫f(x)dx,
b) dosazení do vzorce 
= [F(x)]
≡ F(b) - F(a).
b
a
V našem případě mají tyto kroky následující podobu:
a) Výpočet primitivní funkce F(x) = ∫f(x)dx (Použijeme Mathematicu.)
b) 
= (1 - ArcTan[1]) - ( -1 - ArcTan[-1])
I tento krok přenecháme Mathematice:
V Mathematice není nutno počítat určité integrály ve dvou krocích. Určitý integrál lze spočítat přímo:
Příklad 2
Vypočítejte integrál 
Řešení
a) Vypočteme neurčitý integrál 
dx.
b) 
= 
- 
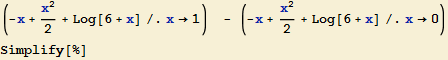
Určitý integrál lze rovněž spočítat přímo:
Příklad 3
Vypočítejte 
.
Řešení
Příklad 4
Vypočítejte 
Řešení
